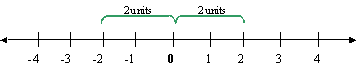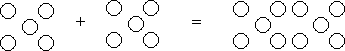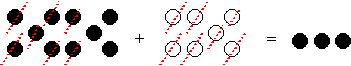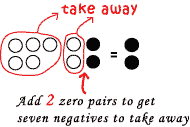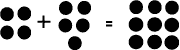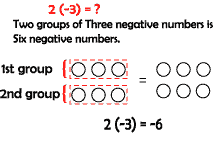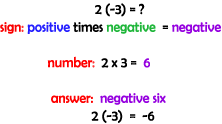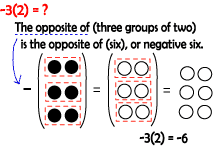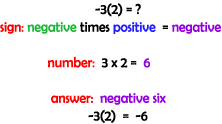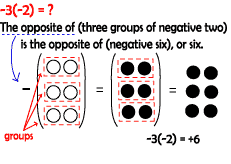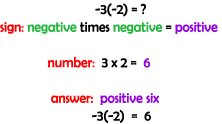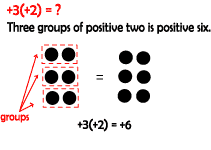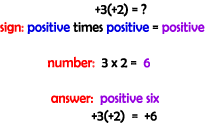[Integers]  [Finding Opposites]  [Absolute Values]  [Addition]  [Subtraction]  [Multiplication/Division]

 
  Numbers called Integers

Numbers greater than zero are called positive numbers.  In some situations, numbers are needed to represent values that are less than zero.  These numbers are called negative numbers.  Positive numbers and negative numbers are called signed numbers.  When the "+ symbol", or "no symbol" is in front of a number, the number is a positive number.  When a single "- symbol" is in front of a number, the number is a negative number.  The number zero ( "0" ) is neither positive nor negative.  The group of numbers called "Integers" have some positive numbers, zero, and negative numbers as seen on the number line below. 

Integers are:  { ..., -3, -2, -1, 0, 1, 2, 3, ... }

A number line:

When using the number line to COMPARE numbers, the number to the:

• LEFT is LESSER (smaller) number, and

•  Right is greater number

Left Number < Right Number

Examples:  

-4  <  2    Negative four is less than two (-4  is left of  2 on the number line)

-4  <  0   Negative four is less than zero (-4  is left of  0 on the number line)

 0  <  2    Zero is less than two (0  is left of 2 on the number line)

 1  <  4  One is less than four  (1  is left of 4  on the number line)

-4  < -1  Negative four is less than negative one (-4 is left of  -1 on the number line)

Compare the following numbers and order from least to greatest.

Given:  { 0, 3, -3, 3.5, -3.5, 5, -5 }

Solution:   -5,  -3.5,  -3,  0,  3,  3.5,  5

[Top]

  Finding OPPOSITES

2 is the opposite of –2, written mathematically:   2 = - (-2)

Examples:  

What is the opposite of:

• 4.75 ?   Answer:  -4.75

• -30  ?  Answer:  +30

• x  ?    Answer: -1x

• 0  ?    Answer: “Trick question” zero is not positive or negative.  
                       Zero has no sign

[Top]

  Absolute Value

The absolute value of a number is the distance from the number on the number line to the zero on the number line.  The symbol for absolute value is |   |.  For:  | 2 | , it is read as “the absolute value of two”.  The absolute value symbols "behave" similarly to parentheses, so, if there is an expression inside the symbols, the order of operations is used to simplify the inside expression before the absolute value can be found.

|-2| = 2  and  |2| = 2,  which says the distance from negative two, or positive two, to the zero-mark  is two units.

** Absolute values are always positive values (because you can’t have a negative value for distance) except when you are already at zero on the number line.

NOTE: If the negative sign is on the outside of the absolute value signs, you are being asked to find the opposite of ‘whatever’ is inside the absolute value signs.

| -2 |  =  2
The absolute value of negative 2 is 2.
  
| 3 + 1 | = | 4 | = 4
The absolute value of ( 3+1 ), which is the absolute value of 4, which equals 4.
  
- | -5 |  =  - (5)  =  -5
The opposite of the absolute value of negative five, which is the opposite of 5, which equals negative five.
 
| 6(5) - 9(7) |  =  | -33 | = 33
The absolute value of [ 6(5) - 9(7) ], which is the absolute value of negative 33, which equals 33.
 
-3 | 4 - 6 |  =  -3 | -2 | = -3 ( 2 ) = -6
The opposite of 3 times the absolute value of [ 4 - 6 ], which is the opposite of 3 times the absolute value of negative 2, which is the opposite of 3 times 2, which equals negative 6.

[Top]

  Adding Integers

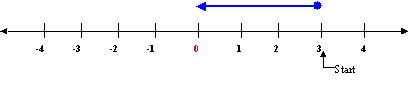
(Method I:  Using a Number Line)

The number line can be used to add integers:  Start on the number line at the first number, then move to the right for adding a positive value, or, move to the left to add a negative value.

Add: -3 + 5  =  2   (Adding 5 positive units, move right 5 units)

Add:  3 + -3 = 0    (Adding 3 negative units, move left 3 units)

(Method II:  Using the “Dot Method”.)

Another method to consider in the investigation of integers is the “Dot method”.

For this method, positive numbers are represented by colored-in dots and negative numbers are represented with white, hollow dots.  A pair (one black/one white) is known as a “zero pair” because they “cancel” each other out, or give a 'zero value'. 

Adding:

• Combining the same colored dots yields more of that dot. 
• Combining different dot types have zero pairs form ("cancel"), resulting with “left-over” dots that yield the solution.

Examples
 Solve.

[Top]

  Subtraction of Integers

The subtraction of integers is not as 'familiar' as one may first believe.  The process of subtraction is still the "taking away" of something.  Up until now, the first number in the subtraction questions were always "bigger" than the amount being taken away. Now, there is the possibility of starting with an amount "too small" to draw away from, or possibly the wrong type of integer to draw away from in the question.  With the introduction of integers, there are now several different situations you may find in a subtraction statement.

Number Line method

Using the number line to subtract integers can be confusing, especially since the number line is a tool best used with addition of integers.  When using a number line to subtract, it is best to learn to rewrite the subtraction statement as an addition statement (see "S-O-O" method below), then obtain your result from adding on the number line tool.

The "S-O-O" method

The "S-O-O" method is a way of changing a subtraction question into an addition question mathematically.  This doesn't change the result in any way, but rather uses patterns to rewriting a question into another question that may be "easier" to solve.

For example, from our experiences with subtraction and integer addition, a pattern is found to change subtraction questions into addition questions:

Examples:

Subtract.
A)    7 – 5   [Seven take away five]

=  7 + (– 5)  [ is the same as, Seven add negative five]

= 2  [the result]

B)     –8 –  (–5)  [Negative eight take away negative five]

  =  –8 + (+ 5)  [ is the same as, negative eight plus positive five]

  =  – 3 [the result]

Recognizing and using the pattern above, a general process can be stated:

"Subtraction statements can be rewritten into addition statements if you: keep the first number and its sign the same, then change the subtraction operation to its opposite operation of  addition, then change the next number to it's opposite sign."

Now, when encountering a subtraction question, it may be solved as rewriting it into an addition statement and combining the numbers. 

The "S-O-O" process is used on a subtraction sentence by:
           (“S – O – O” means “Same – Opposite – Opposite”)

• S:  Keep the first number with its sign, the SAME
• O:  change to the OPPOSITE operation (ADDITION)
• O: Change the number following the operation change to its OPPOSITE sign.

Examples:

Solve.

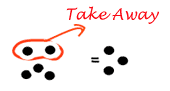
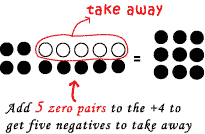
The DOT Method

Using  "dots" with an assigned sign is one way to visualize the subtraction of integers.  Probably the easiest way to achieve the correct solution is by first doing the "S-O-O" method, or rewriting all subtraction statements into addition statements, and then combining the numbers to arrive at the correct solution.

Another way to use the dots is to model it with the appropriate dots and if the amount needed to take away is not present, zero pairs are added to the model until the desired amount is present, then subtraction (taking away) can occur.  The "left over" dots indicate the correct result to the integer subtraction statement.

Examples:

Solve.

A)    5 – 2 = ?

S-O-O method  5 –  2  =  ? 5 + (-2)  =  3	Take away (No zero pairs needed) 5 –  2  =  3

 
B)    -5 – (-3) = ?

S-O-O method  -5 –  (-3)  =  ? -5 + (+3) = -2	Take away (No zero pairs needed) -5 – (-3) = -2

  
C)   –5 – ( –7 ) = +2

S-O-O method  –5 – ( –7 ) = ? –5 + ( +7 ) = +2	Take away (Two zero pairs needed) –5 – ( –7 ) = +2

   
D)   4 – (– 5) =  ?

S-O-O method  4 – (– 5)  =  ? 4 + (+ 5)  =  +9	Take away (Five zero pairs needed) 4 – (– 5)  = +9

[Top]

  Multiplication and Division of Integers

Multiplying and Dividing Integers will have two parts to consider: the sign of the solution, and the numerical aspect of the solution.  With signed numbers, it is important to determine both the numerical part as well as the sign of the solution, in  multiplication and division questions.

Multiplying with Integers

Remember:

• A negative symbol means: “the opposite of”
• Multiplying is a “quick adding” of numbers

Looking at some examples of multiplying integers, a pattern to apply to all multiplication questions will be found.

Examples

Multiply.

A)   2 ( -3) = ?

"Dot Picture"	Pattern

B)   -3 (2)  =  ?

"Dot Picture"	Pattern

C)   -3 (-2) = ?

"Dot Picture"	Pattern

D)   +3 (+2) = ?

"Dot Picture"	Pattern

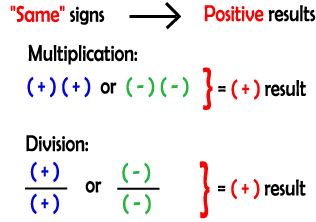
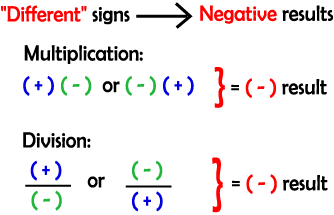
Focusing on the "Pattern" side of the examples (above), it is seen that finding the "sign of the solution" depends on the signs of the numbers being multiplied, and the "numerical aspect" of the solution depends on just the numbers being multiplied (does not depend on the sign).  To get a positive solution, the signs of the numbers being multiplied have to be the same.  To get a negative solution, the signs of the numbers being multiplied have to be different.

Division with Integers

The patterns found in dividing integers are the same as seen in multiplying integers.  The sign of the solution follows the pattern stated above and the numerical part of the answer depends upon the numbers being divided.

• To get a positive solution,
  the numbers being divided have to be of the same sign.

• To get a negative solution, 
  the numbers being divided have to be of  different signs.

The two boxes below give the general rules to remember when Multiply or Dividing numbers with the same signs and with different signs.
 

Examples
Solve.